Триггеры, сумматоры, да и просто логические схемы, таблицы истинности… — натуральная головная боль любого преподавателя информатики. Весь урок пропрыгаешь перед доской объясняя, а в головах у учеников практически ничего не остается. К счастью, теперь появился удобный инструмент, как для демонстрации, так и практического закрепления этой темы. Я имею ввиду программу Logisim, которая написана на java и работает «из коробки»1 практически сразу после скачивания с sourceforge.net2. Интерфейс программы русский, если, конечно, у пользователя правильно установлена русская локаль.
Олег Чебан из Алтайского края работает в колледже и использует Logisim на занятиях по «Цифровой схемотехнике», цель которой исследовать и проектировать цифровые схемы (не электрические), для специальности «автоматика». Олег разработал целый цикл лабораторных работ. Вот одна из них, которая дает представление и о возможностях программы Logisim и о способе применения ее в школе или в среднем профессиональном образовании.
Лабораторная работа №9. Построение двоичного сумматора в программе Logisim.
Цель работы:
Изучение правил выполнения арифметических действий над двоичными числами и исследование принципов построения двоичных сумматоров.
Ход работы.
Основным элементом, используемым в двоичных арифметических элементах, является полусумматор. Начнем с так называемой схемы сравнения:
1. Запустите программу Logisim (автор использует ver. 2.7.1)
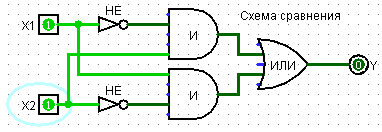
2. С помощью «Панели инструментов» постройте схему сравнения, см. Рис. 1.
Рис. 1
3. С помощью «Таблицы атрибутов» задать метки: вход X1 и X2, логические И, ИЛИ и НЕ, выход Y.
4. Проводник — Базовые — Инструмент Текст: Подписать схему, как «Схема сравнения».
5. С помощью инструмента «Изменять значения в схеме» 
поэкспериментируйте с подачей на входы X1 и X2 логической единицы 1 и логического 0
6. По команде: Проект — Анализировать схему получить Таблицу истинности схемы сравнения, см. Рис. 2.
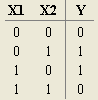
Рис. 2
Комментарий. Схема сравнения получает младший разряд числа при сложении двух двоичных чисел (бит) без учета переноса! Например: 1 + 1 = 0 младший разряд, перенос 1.
7. С помощью инструмента «Добавить схему» 
добавим схему «Полусумматор», см. Рис. 3.
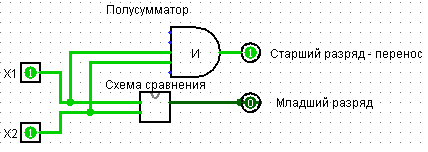
Рис. 3
Схему сравнения заимствуем с панели проводника >>>
8. Проект — Анализировать схему — получить Таблицу истинности полусумматора, см. Рис. 4.
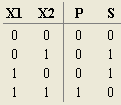
Рис. 4
Комментарий. Схема позволяющая складывать два двоичных числа (бит) называется полусумматором. В нашем случае P – перенос, S – младший разряд, остаток. Однако, при сложении двух двоичных чисел недостаточно использовать полусумматор, т. к. полусумматор не имеет входа для учета переносов из других разрядов.
9. Добавить схему «Сумматор»
10. Используя подсхему «Полусумматор» построить «Сумматор», см. Рис. 5.
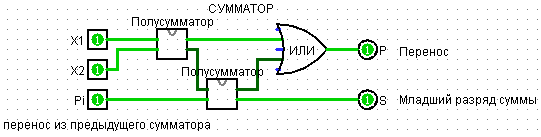
Рис. 5
11. По команде: Проект — Анализировать схему получить Таблицу истинности «Сумматора», Рис. 6.
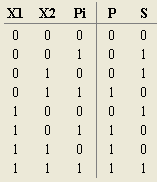
Рис. 6
12. Построим схему из 4-х сумматоров, которые позволят складывать два четырехразрядных числа.
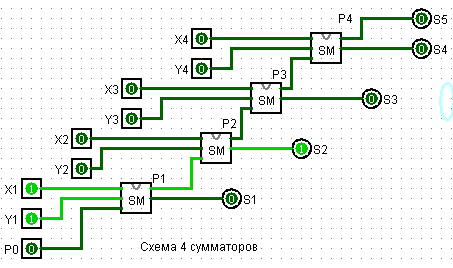
Рис. 7
Где:
- X1 и Y1 слагаемые первого сумматора, X2 и Y2 – второго и т. д.
- S1, S2, S3 .. S5 – младший разряд суммы
- P1, P2, P3 и P4 – перенос, старший разряд сумматора 1, 2, 3 и 4
- P0 – всегда равно 0, т. к. в первом сумматоре складываются первые двоичные числа X1 и Y1, переноса нет.
В нашем примере выполняем сложение двух четырехразрядных чисел: 0001 + 0001 = 00010
| X4 | X3 | X2 | X1 | |
| + | Y4 | Y3 | Y2 | Y1 |
| S5 | S4 | S3 | S2 | S1 |
| 0 | 0 | 0 | 1 | |
| + | 0 | 0 | 0 | 1 |
| 0 | 0 | 0 | 0 | 0 |
13. Проверить схему при следующих входных данных:
| 1 | 0 | 0 | 1 | Xi | |
| + | 0 | 0 | 1 | 1 | Yi |
| 0 | 1 | 1 | 0 | 0 | Si |
Самостоятельно. Построить схему позволяющую складывать 8 разрядов двоичных чисел.
Приложение файл программы для Logisim: Сумматор.circ.
———
1Если запускать программу из каталога содержащего jar-файл (например logisim-generic-2.7.1.jar), то строка запуска может выглядеть так:
java -jar ./logisim-generic-2.7.1.jar
2 Пользователи дистрибутивов Альт Линукс могут скачать программу из соответствующего репозитария.
, тип 1 байт
"+2)
